Part A
The solid formed by the net has a bottom and a top face which are rectangles with a width of 3 and a length of 4.
Also, it has four lateral faces which are rectangles: two with a length of 4 and a width of 2, and the other two with a length of 3 and a width of 2.
Notice that the width of the lateral faces corresponds to the height of the solid.
Thus, the solid is a rectangular prism, with dimensions:
• length: 4
,
• width: 3
• height: 2
Part B
A similar solid with an enlargement ratio of 2 changes the length, width, and height of the solid to: 8, 6, 4.
For an enlargement ratio of 1, the dimensions stay the same.
For an enlargement ratio of 3, each dimension is multiplied by three.
For an enlargement ratio of 4, each dimension is multiplied by four.
Part C
The volume of a rectangular prism is the product of its three dimensions. So, when we enlarge each of its dimensions by a linear scale factor of 10, the volume is changed as follows:
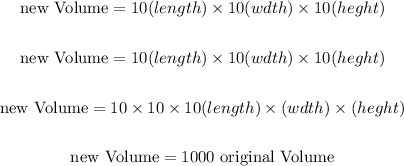
Therefore, the volume increases 1000 times.
And if the solid is enlarged by a linear scale factor of r, we have:
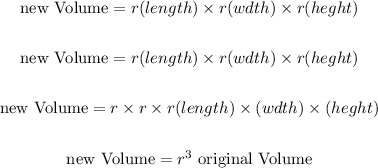
Therefore, the volume increases by a factor of r³.