Question

aA ball is launched from a 137.2-meter tallplatform. The equation for the ball's height h attime t seconds after launch ish(t) = -4.9t2 + 2.94t + 137.2, where h isin meters. When does the object strike theground?=

Answer 1

We need to find the value of t for which h(t) = 0.

Notice that a quadratic equation may have two real solutions. Since t starts at 0 and only grows, we are interested in the positive solution only.

We have:

`\begin{gathered} h(x)=0 \\ \\ -4.9t^2+2.94t+137.2=0 \end{gathered}`

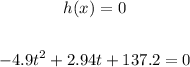
Then, using the quadratic equation, we obtain:

`\begin{gathered} t=(-2.94\pm√((2.94)^2-4(-4.9)(137.2)))/(2(-4.9)) \\ \\ t=(-2.94\pm√(8.6436+2689.12))/(-9.8) \\ \\ t=(2.94\pm√(2697.7636))/(9.8) \\ \\ t=(2.94\pm51.94)/(9.8) \\ \\ t_1=(2.94-51.94)/(9.8)=-5 \\ \\ t_2=(2.94+51.94)/(9.8)=5.6 \end{gathered}`

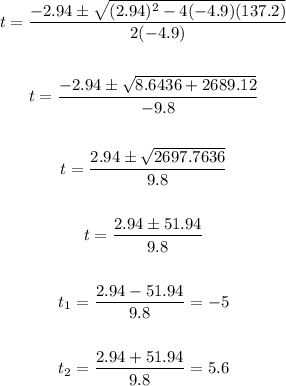
Answer

The object strikes the ground at: t = 5.6 seconds.