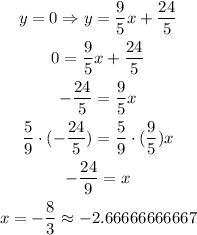To sketch this line equation, it would be a good idea to write the equation of the line in the slope-intercept form first.
Finding the equation of the line in slope-intercept form
The equation of the line in the slope-intercept form is given by:

Where:
• m is the slope of the line.
,
• b is the y-intercept of the line (the point where the line passes through the y-axis. At this point, x = 0.
Now, we have that the line equation is given in point-slope form as follows:
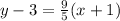
We can multiply both sides of the equation by 5:
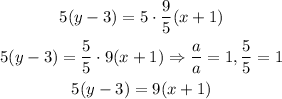
Now, we have to apply the distributive property to both sides of the equation:
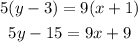
Add 15 to both sides of the equation, and then divide by 5:
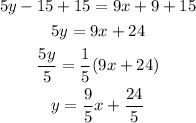
Therefore, the equation is slope-intercept form is:
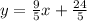
Sketching the graph for the line
Since we have that the original equation of the line was:
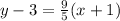
We already know that one of the points of the line is (-1, 3) since the point-slope form of the line is given by:
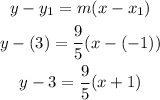
We need another point to graph the line. We can use the y-intercept obtained before:
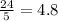
And since we know it is the y-intercept, we have that this point is (0, 4.8). Therefore, we can graph this equation using the following points:
(0, 4.8) and (-1, 3). Then we can sketch the line as follows:
To have a more precise graph for the line, we can use a graphing calculator:
We can see that the line passes through the x-axis at the point: