Question

Write 2 sine equations and 2 cosine based on the triangle

Answer 1

We are given a right triangle with a known hypotenuse and two unknown sides.

We will determine the values of "x" and "y". First, we will determine the value of "x". To do that we will use the function cosine for the angle of 24 degrees. The function cosine is defined as:

`\cos \theta=(adjacent)/(hypotenuse)`

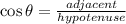
The adjacent side is the side that is next to the angle and the hypotenuse is the side that is opposite to the 90 degrees angle. Now, we substitute the values:

`\cos 24=(x)/(7)`

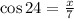
Now, we solve for "x" by multiplying both sides by 7:

`7\cos 24=x`

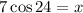
Solving the operations:

`6.4=x`

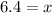
Therefore, the side "x" is 6.4.

Now, we use the function sine to determine the side "y". The sine function is defined as:

`\sin \theta=\frac{\text{opposite}}{\text{hypotenuse}}`

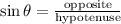
Now, we substitute the values:

`\sin 24=(y)/(7)`

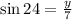
Now, we multiply both sides by 7:

`7\sin 24=y`

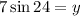
Solving the operations:

`2.84=y`

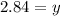
Therefore, the value of "y" is 2.84.

The same procedure can be used for the 66 degrees angle to get two additional equations of sine and cosine. These equations would be redundant since we would get the same values of "x" and "y".