Question

A line passing through which of the following pairs of coordinates represents a proportional relationship?

A. (1, 3) and (3, 6)
B. (2, 5) and (4, 6)
C. (2, 4) and (5, 6)
D. (3, 6) and (4, 8)

Answer 1

D since the y-intercept would be (0,0), which means that it starts from the origin.
(haha I misread option A and B)

Answer 2

D. (3, 6) and (4, 8)

Explanation:

A proportion relation is defined as two variables that interact one to each other, directly. Basically its definition could be

`y=kx`

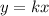
This means that the set of points must have a constant proportion
`k`.

However, in this case we only have one pair of points. A specific characteristic of proportional relationship in this case is that such ratio is a whole number: ±1, ±2, ±3, ±4, ±5,... ±n.

In this case, the last pair of point fulfil this characteristic. We demonstrate that by finding the ratio, which is the slope of the linear relationship

`m=(y_(2)-y_(1) )/(x_(2)-x_(1) )`

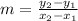
Where
`(x_(1) ,y_(1) )` is the first point and
`(x_(2) ,y_(2) )` is the second point. Replacing these points, we have

`m=(8-6)/(4-3)=(2)/(1)=2`

So option D has a proportional relationship with a constant ratio of 2.