Let's find the values of x and y.
Take the following steps:
Step 1:
Apply the equation below to find x
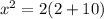
Let's solve for x.
Apply distributive property:
![\begin{gathered} x^2=2(2)+2(10) \\ \\ x^2=4+20 \\ \\ x^2=24 \\ \\ \text{Take the square root of both sides:} \\ \sqrt[]{x^2}=\sqrt[]{24} \\ \\ x=4.9 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/rpwbxxey88j493ji8cjp.png)
Step 2:
Apply the equation below to find the value of y
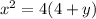
Substitute 24 for x² and find the value y:

Divide both sides by 4:
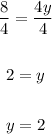
Therefore, we have:
x = 4.9
y = 2
ANSWER:
x = 4.9