So,
Given the function:
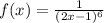
We want to find the equation of the tangent line to this function at the point x=2.
The first thing we need to do, is to find the deritative of the function.
We could use the quotient rule as follows:
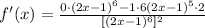
If we rewrite:

Now, we need to find the value of the deritative of this function at the point x=2. That's because that's the slope of the tangent line at that point.
So,

Then, we could use the fact that the equation of a line can be found using the following:

Where (x1,y1) is a point that lie on the line and m is the slope.
We got that x1 = 2, and the value of y1 will be the value of f(x) when x=2:
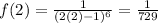
Therefore, the point is (2 , 1/729).
Finally, we replace all these values in the equation given:
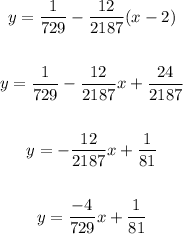
And that's the equation of the tangent line to that function at the point x=2.