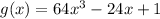Question

let the graph GPA horizontal shrink by a factor of four, followed by a translation two units up of the graph of f(x)=x^3-6x-1

Answer 1

By the rules of transformation of functions, you know that

*f(bx), where b>1, the function shrinks the curve horizontally by a factor of b.

*f(x)+k moves the function k units up

So, in this case, you have

*b=4 and

*k=2

`\begin{gathered} g(x)=f(bx)+k \\ g(x)=f(4x)+2 \\ f(x)=x^3-6x-1 \\ g(x)=(4x)^3-6(4x)-1+2 \\ g(x)=64x^3-24x+1 \end{gathered}`

To verify you can graph the functions f(x) and g(x), like this

Therefore, the function g(x) is

`g(x)=64x^3-24x+1`