Question

In the diagram below of triangle ABC, D is a midpoint of AB and E is a midpoint of BC. If mZDEB = 119 - 7x, and mZACE = 101 - 5x, what is the measure of ZACE? B D E A С

Answer 1

We want to find the measure of the ∠ACE. For doing so, we are going to use some geometrical properties with the information given.

As D is the midpoint of AB, we have that:

`AD\cong DB`

And as E is the midpoint of BC, we have:

`BE\cong EC`

Moreso, we can say that:

`(AB)/(DB)=(BC)/(BE)=2`

And thus, the sides are proportional. As both triangles have the angle:

`\angle DBE\text{ which is the same as }\angle ABC`

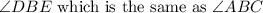
We can say that the triangles ABC and DBE are similar by the Theorem SAS (side-angle-side):

`\begin{gathered} \text{Side 1: }AB\approx DB \\ \text{Angle: }\angle DBE \\ \text{Side 2: }CB\approx EB \end{gathered}`

Thus, their sides are proportional, and their corresponding angles are congruent.

As the angles ACE and DEB are corresponding (on the two triangles), they have the same measure:

`\begin{gathered} m\angle ACE=m\angle DEB \\ 101-5x=119-7x \\ \text{And we solve for x:} \\ 101-5x+7x=119-7x+7x \\ 101+2x=119 \\ 2x=119-101 \\ 2x=18 \\ x=(18)/(2)=9 \end{gathered}`

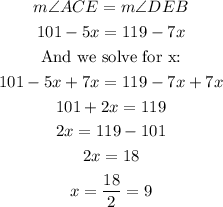
This means that the value of x is 9. Now, replacing on the value of ACE, and we get:

`\begin{gathered} m\angle ACE=101-5x \\ =101-5(9) \\ =101-45 \\ =56 \end{gathered}`

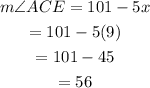
Thus, the value of the angle ∠ACE is 56°.