Question

Consider the following function.f(x) = 6 − |x − 8|(a) Find the critical numbers of f. (Enter your answers as a comma-separated list.)....c) Apply the First Derivative Test to identify the relative extremum. (If an answer does not exist, enter DNE.)relative maximum (x, y) =

Answer 1

Okay, here we have this:

Considering theprovided function, we are going to find the critical numbes of f, and identify the relative extremum, so we obtain the following:

So let us recall that a number a is a critical value of f if f '(a) = 0 or f ' is undefined at x = a. Then let's derive the function to know the critical points:

`\begin{gathered} f^(\prime)(x)=(d(6-|x-8|))/(dx) \\ =(-(x-8)/(|x-8|)) \\ =-(x)/(|x-8|)+(8)/(|x-8|) \end{gathered}`

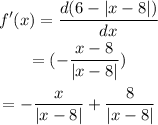
We can see that the derivative is not defined at 8 because this value makes it indeterminate, so this is the critical value of the function.

c)

Now to find the relative extremum, we will then evaluate f'(x) to the left and right of the absolute value:

Then we will evaluate f'(x) at x=7 and x=9:

x=7, x=9:

`\begin{gathered} f^(\prime)(7)=-(7)/(|7-8|)+(8)/(|7-8|) \\ =-(7)/(1)+(8)/(1) \\ =-7+8 \\ =1 \end{gathered}`
`\begin{gathered} f^(\prime)(9)=-(9)/(|9-8|)+(8)/(|9-8|) \\ =-(9)/(1)+(8)/(1) \\ =-9+8 \\ =-1 \end{gathered}`

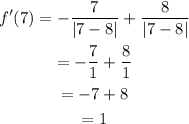
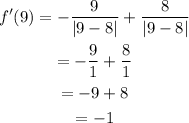
As when evaluating it gave us that it is greater than zero on the left and less than zero on the right, then it is a local maximum.

And the maximum is:

`\begin{gathered} f(8)=6-|8-8| \\ f(8)=6-0 \\ f(8)=6 \end{gathered}`

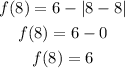
Finally we obtain that the relative maximum is (8, 6).