Final mixture: 90oz of 85% salt:
Find the 85% of 90 to know the ounces of salt in the final mixture:
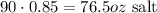
If A is the ounces of solution A and B the ounces of solution B, the sum of A and B is equal to 90oz:
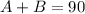
The quantity of salt in solution A is 0.7A, the quantity of salt in solution B is 0.95B. The sum of 0.7A and 0.95B needs to be 76.5 (Total quantity of slat in the final mixture):
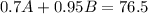
______
Use the next system of linear equations to find A and B:
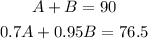
1. Solve A in the first equation:
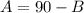
2. Substitutet he A in the second equation by the value you get in step 1:
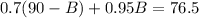
3. Solve B:
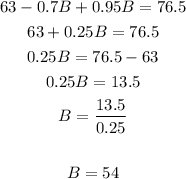
4. Use the value of B to find A:
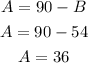
Then, to get a final mixture of 90oz of 85% salt you use 36 ounces of solution A and 45 ounces of solution B