We are looking at the price of the senior citizen ticket and the price of the student ticket. Knowing the total sales from the first day and second day, we can solve this problem by using a system of equations.
We let x be the price of the senior citizen ticket while y be the price of the student ticket. On the first day, the school sold 10 senior citizen tickets and 14 student tickets. The total sales are $200. We can represent this in equation form as
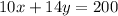
For the second day, the school sold 9 senior tickets and 7 student tickets, with a total sales of $152. This can be represented in a mathematical expression as
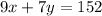
Hence, we now have our system of equations written as
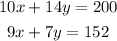
Let's solve for the values of x and y using the elimination method. I will multiply -2 on the second equation so that y can be eliminated. We now have
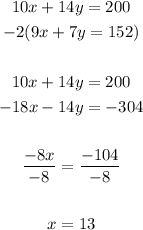
We can use this value of x and substitute it on either of the equation present in the system of equations. In this case, I will be using the first equation. We have
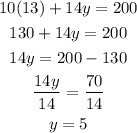
Hence, the price for the senior citizen ticket is $13 while the price for the student ticket is $5.
Answer:
Senior citizen ticket price = $13
Student ticket price = $5