Step-by-step explanation:
We can use the substitution method to solve this system.
First we clear y from the first equation:
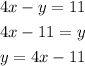
Then we replace this expression into the second equation:
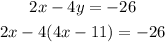
Solve for x:
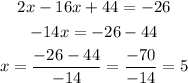
And with x = 5 we replace it into the first equation and solve for y:
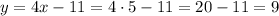
Answer:
The solution is (5, 9)