Given the data in the image, the data can be gotten using the general rule for stem and leaf which states that: A stem and leaf is a table used to display data. The 'stem' is on the left displays the first digit or digits. The 'leaf' is on the right and displays the last digit. For example, 543 and 548 can be displayed together on a stem and leaf as 54 | 3,8.
Step 1: Using the explanation above, our data can be written out as below:
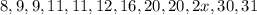
Step 2: Write out the formula for the interquartile range which equals 12.
![\begin{gathered} \text{IQR}=Q3-Q1 \\ \text{where Q3 equals the median of the half of the data to the right} \\ \text{and Q1 equals the median of the half of the data to the left} \\ To\text{ get Q3:} \\ (16,20,20,2x,30,31)_{} \\ \operatorname{median}=(20+2x)/(2) \\ To\text{ get Q1:} \\ (8,9,9,11,11,12) \\ \operatorname{median}=(9+11)/(2)=(20)/(2)=10 \end{gathered}]()
Step 3: We equate the formula for interquartile range to 12, we let 2x=y to ease the solution steps:
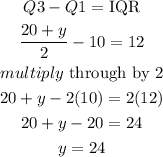
Step 4: Recall that 2x=y, this means 2 and a number =y. We then equate the number 2x to y since we have gotten the value for y. This means;
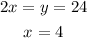
Hence, the value for x is 4.