Question

Find the sum of the all the multiple of 3 beta between 100 and 301 cinclusives which are multiples of 3.

Answer 1

Answer: 13,467

Step-by-step explanation:

The first multiply of 3 after 100 is 102 (102/3 = 34) and the last multiple of three before 301 is 300 (300/3 = 100).

So, we can organize the multiples of 3 in a sequence: (102, 105, ..., 297, 300).

As we can see, we have an arithmetic sequence above, with the following parameters:

first term = a1 = 102

last term = an = 300

number of terms = n = ?

common difference = d = 3

First, we have to find the number of terms of this sequence. To do this, we can use the following formula:

`\begin{gathered} an=a_1+(n-1)\cdot d \\ 300=102+(n-1)\cdot3 \\ 300-102=(n-1)\cdot3 \\ 198=(n-1)\cdot3 \\ (198)/(3)=n-1 \\ 66=n-1 \\ 66+1=n \\ n=67 \end{gathered}`

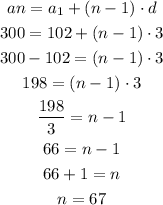
Now, we can use the formula for the sum (S) of the arithmetic sequence and find the sum of the terms:

`\begin{gathered} S=(n\cdot(a_1+an))/(2) \\ S=(67\cdot(102+300))/(2) \\ S=13,467 \end{gathered}`

The sum is 13,467.