Question

44. Consider the equation 4 (x-8) + y = 9(x-2).[Part 1]Find an expression for y of the form ax+b expression for y such that the equationhas infinitely many solutions. Is there more than one such solution? Explain yourreasoning using complete sentences.[Part 2]Find an expression for y of the form ax+b expression for y such that the equationhas no real solutions. Is there more than one such solution? Explain yourreasoning using complete sentences.

Answer 1

• 1. y=5x+14

,

• 2. y=5x+30

Explanation:

Given the equation:

`4(x-8)+y=9\left(x-2\right)`

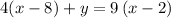
To answer the given questions, first, make y the subject of the given equation.

`\begin{gathered} 4(x-8)+y=9(x-2) \\ y=9(x-2)-4\left(x-8\right) \\ y=9x-18-4x+32 \\ y=9x-4x-18+32 \\ y=5x+14\cdots(1) \end{gathered}`

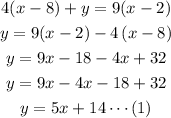
Part 1

We want to find an expression of the form y=ax+b such that the equation has infinitely many solutions.

A system of equations has infinitely many solutions if the two equations in the system simplify to the same line.

Thus, we find an equation that is a multiple of the simplified equation (1) above.

Multiply equation 1 all through by 1.

`\begin{gathered} (y=5x+14)*1 \\ y=5x+14\cdots(2) \end{gathered}`

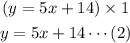
Thus, the system of equations:

`\begin{gathered} y=5x+14\cdots(1) \\ y=5x+14\cdots(2) \end{gathered}`

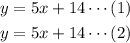
This system has infinitely many solutions since they simplify to the same line.

Part 2

We want to find an expression of the form y=ax+b such that the equation has no real solutions.

For a system of equations to have no real solutions, the two lines formed by the equations must be parallel.

This means that they must have the same slope.

In equation 1:

`y=5x+14\cdots(1)`

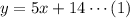
The slope is 5.

Thus, find another equation that also has a slope of 5.

`y=5x+30\cdots(3)`

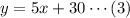
The system of equations below has no real solutions.