Answer:
• Width: 56 yards.
,
• Length: 232 yards.
Step-by-step explanation:
Let the width of the rectangular field = w
Quadruple the width = 4w
The length is 8 yards longer than quadruple the width. Therefore:
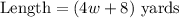
The perimeter of the field is 576 yards.
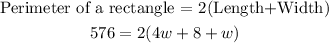
We solve the equation for w.

The width of the rectangular playing field is 56 yards.
Next, we find the length.
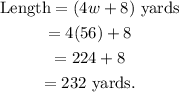
The length of the rectangular playing field is 232 yards.