Answer:
a. 5:6 and 25:36
Step-by-step explanation:
Step 1. In the figure, we have two similar triangles. Since they are similar, there is a proportion or ratio between their sides.
We are required to find the ratio of the perimeter and the ratio of the area.
Step 2. The sides 15 and 18 are corresponding sides (there is a proportion between them), and we can write the ratio of the sides as follows:
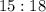
Simplifying both numbers by dividing them by 3:
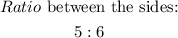
Step 3. The ratio of the perimeters is the same as the ratio between the sides:
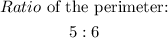
Step 4. To find the ratio of the areas we square the two numbers from the ratio of the perimeters:
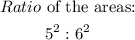
The result is:
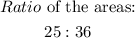
Answer: a.
5:6 and 25:36