Question

A daring squirrel runs toward a cat, then turns around to safety. A graph of its velocity over time is shownbelow.

Answer 1

a) In order to graph acceleration vs time, it is necessary to calculate acceleration for four different time intervals. Use the following formula for the acceleration:

`a=(v-v_o)/(t)`

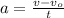
where v is the final speed and vo is the initial speed.

Between t=0.0 and t=0.5 you have for a:

`a=(4-2)/(0.5)(m)/(s^2)=4(m)/(s^2)`

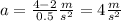
Between t=0.5 and t=1.0:

`a=(4-4)/(0.5)(m)/(s^2)=0(m)/(s^2)`

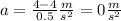
Between t=1.0 and t=2.0:

`a=(-2-4)/(1.0)(m)/(s^2)=-6(m)/(s^2)`

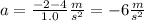
Finally, between t=2.0 and t=2.5:

`a=(0-(-2))/(0.5)(m)/(s^2)=4(m)/(s^2)`

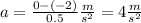
Then, with the previous values of the acceleration you have the following

a vs t graph:

b) In order to graph position vs time for the first second of motion, use the following formula for position x:

`x=v_ot+(1)/(2)at^2`

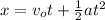
Consider that between t=0 and t=0.5 the acceleration is 4m/s^2 and the initial speed is 2m/s, then, you have for this time interval:

`\begin{gathered} x=(2(m)/(s))(0.5s)+(1)/(2)(4(m)/(s^2))(0.5s)^2 \\ x=1.5m \end{gathered}`

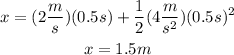
Between t=0.5 and t=1.0 the acceleration is zero, then, the speed of squirrel is constant (4m/s). The value of the final position is then:

`x=vt=(4(m)/(s))(0.5s)=2m`

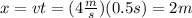
In order to graph position vs time, consider that in the first time interval you have a parabolla (there is an acceration) and in the second interval you have a line (constant speed):