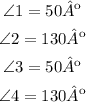Question

on the diagram shown of two intersecting lines if the angle of 2 equal 130 degree what would the degree of angles at 1, 3 and 4 equal

Answer 1

In the diagram shown in the picture, both lines intersect forming 4 angles.

The angles that share a vertex but not sides, meaning that they are on the opposite side of the X shape, are vertically opposite angles:

Vertically opposite angles are equal so that:

∠1=∠3

∠2=∠4

We know that ∠2= 130º, since ∠4 is equal to ∠2, then ∠4= 130º

Now ∠1 and ∠2 are on the same line, which means that they are a linear pair.

Linear pairs are adjacent supplementary angles, which means that their sum is equal to 180º

Knowing this we can calculate the measure of ∠1 as follows:

`\begin{gathered} \angle1+\angle2=180º \\ \angle1+130=180 \\ \angle1=180-130 \\ \angle1=50º \end{gathered}`

Finally, ∠1 and ∠3 are equal so ∠3=50º

So the measures for the angles are:

`\begin{gathered} \angle1=50º \\ \angle2=130º \\ \angle3=50º \\ \angle4=130º \end{gathered}`