Question

Quadrilateral ABCD with points A (2, -1) , B (4, -4), C (2, -7), D (0,-4) is shown below. Write the equations of line symmetry in quadrilateral ABCD. Explain your reasoning.

Answer 1

Given

A Quadrilateral ABCD with points A (2, -1) , B (4, -4), C (2, -7), D (0,-4).

To find the equations of line symmetry in quadrilateral ABCD.

Step-by-step explanation:

It is given that,

From the figure, it is clear that the quadrilateral is a Rhombus.

Since the Rhombus has two lines of symmetry AC and BD.

Therefore,

The equation of the line AC is,

`\begin{gathered} (y-y_1)/(y_2-y_1)=(x-x_1)/(x_2-x_1) \\ (y-(-1))/(-7-(-1))=(x-2)/(2-2) \\ (y+1)/(-7+1)=(x-2)/(0) \\ (y+1)/(6)=(x-2)/(0) \\ x-2=0 \\ x=2 \end{gathered}`

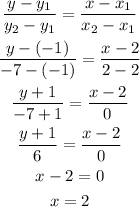
Therefore the equation of the line of symmetry AC is, x=2.

Similarly, the equation of the line of symmetry BD is, y= -4, because BD is a horizontal line.

Reasoning:

Since the lines of symmetry are horizontal line and vertical line.

Hence, x=2, y=-4 are the equations of the lines of symmetry.