Jared's solution was:
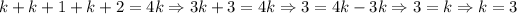
Jared's got the following three integers: 3, 3+1, 3+2, or 3, 4, 5.
The correct solution
First of all. to represent three consecutive even integers whose sum was 4 times the first of those integers is:
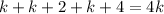
We can find k:
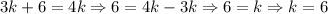
The even integers are then: 6, 6+2, 6+4 or 6, 8, 10.