To find if the data from the sample are consistent with the distributors claims, we first express the number of each type of egg purchased as a percentage of the total number of eggs purchased:
Thus, for the white eggs:
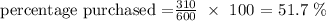
For brown eggs:
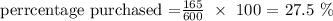
For organic eggs:
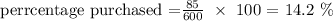
For free-range eggs:
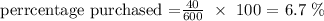
Now, we can see that these percentage values correspond closely with that reported by the distributor: 51.7% compared to 50% for white egg purchases. 27.5% compared to 30% for brown egg purchases, 14.2% compared to 15% for organic egg purchases, and 6.7% compared with 5% for free-range eggs.
Now that we have Observed and Expected percentage values for each type of egg purchase, we can apply the Chi-Square Goodness of fit test to determine whether or not to reject the claims made by the distributor.
We now state the hypotheses as follows.
H0: Distributor's claims are correct.
H1: Distributor's claims are wrong
Now, we have to find the critical value.
Since the degrees of freedom are 4-1 =3, and alpha (significance level) is 0.05 (equivalent of 5%)
Hence, the critical value from Chi-Square tables is 7.815.
Now we compute the test value by subtracting the expected value from the
corresponding observed value, squaring the result and dividing by the
expected value, and then finding the sum.
![\begin{gathered} X^2\text{ = }\sum ^{}_{}((O-E)^2)/(E) \\ X^2\text{ = }((51.7-50)^2)/(50)\text{ + }((27.5-30)^2)/(30)\text{ + }((14.2-15)^2)/(15)\text{ + }((6.7-5)^2)/(5) \\ X^2\text{ = 0.0578 +0.2083 + 0.0427 +0.578} \\ X^2\text{ = 0.8868} \\ \text{Now, since 0.8868 < 7.815, we accept the null hypothesis and conclude that the distrubutor's claims are correct} \end{gathered}]()