SOLUTION
We have been given the equations for supply and demand for sugar as
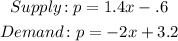
And we want to use this to find the equilibrium demand and equilibrium price.
At equiibrium price, demand and supply are equal. So we will equate the two equations to get x. The x here represents the equilibrium demand.
We have
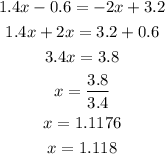
Hence, the equilibrium demand is 1.118
So we can use any of the equations for demand or supply to find the equilibrium price. Using the first equation, we have

Hence, the equilibrium price is approximately 0.96