Question

Last year, Lucy had $30,000 to invest. She invested some of it in an account that paid 8% simple interest per year, and she invested the rest in an account that paid 6% simple interest per year. After one year, she received a total of $1880 in interest. How much did she invest in each account?

Answer 1

Given:

`Pr\text{ incipal= \$30000}`

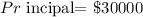
Let x be the principal for the 8% simple interest per year

Let y be the principal for the 6% simple interest per year

Hence,

`x+y=30000\ldots\ldots\ldots\ldots\ldots\ldots(1)`

The formula for calculating simple interest is;

`\begin{gathered} I=(P* T* R)/(100) \\ T=1\text{year} \\ I=(PR)/(100) \end{gathered}`
`\begin{gathered} I_x=(x*8)/(100) \\ I_x=0.08x \\ \\ I_y=(y*6)/(100) \\ I_y=0.06y \\ \\ I=I_x+I_y=1880 \\ 0.08x+0.06y=1880\ldots\ldots\ldots\ldots\ldots(2) \end{gathered}`

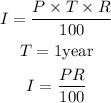
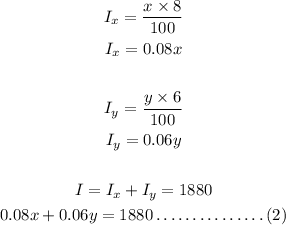
Solving the two equations simultaneously;

`\begin{gathered} x+y=30000\ldots\ldots\ldots\ldots\ldots\ldots(1)*0.08 \\ 0.08x+0.08y=2400\ldots\ldots\ldots\ldots\ldots\ldots.\text{.}(1) \\ 0.08x+0.06y=1880\ldots\ldots\ldots\ldots\ldots\ldots..(2) \\ \text{Subtracting equation (2) from (1);} \\ \text{equaton (1)-equation (2);} \\ 0.02y=520 \\ \text{Dividing both sides by 0.02 to get y,} \\ y=(520)/(0.02) \\ y=26000 \\ \\ \text{Substituting y into equation (1) to get x,} \\ x+y=30000 \\ x+26000=30000 \\ x=30000-26000 \\ x=4000 \end{gathered}`

Therefore,

Lucy invested $4,000 principal for 8% simple interest.

Lucy invested $26,000 principal for 6% simple interest.