We have the general rule for a rotation of 90° counterclockwise:
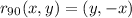
and the general rule for a y=-x reflection is:
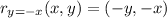
In this case, we have the points R=(2,-2), S=(5,-1) and T=(3,-5).
Then, we first have to use the 90° rotation on all points:
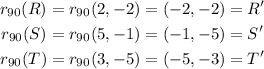
Now we use the y=-x reflection on our new points:
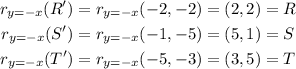
therefore, the final points after the transformations are:
R''=(2,2)
S''=(5,1)
T''=(3,5)