Question

Need help on part c of this problem, thank you in advance.

Answer 1

The solution in interval notation is [-3, -2]

STEP - BY - STEP SOLUTION

What to find?

The solution of the given inequality in interval notation.

Given:

4(x+3) ≥ 0 or 4(x + 4) ≤ 8

Solve the first part of the inequality.

That is;

4(x+3)≥ 0

Open the parenthesis.

4x + 12 ≥ 0

Subtract 12 from both-side of the inequality.

4x + 12 - 12 ≥ 0- 12

4x ≥ -12

Divide both-side of the inequality by 4

`\frac{\cancel{4}x}{\cancel{4}}\ge-(12)/(4)`

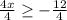
x ≥ -3

Proceed to solve the second part of the inequality.

4(x+ 4) ≤ 8

Open the parenthesis.

4x + 16 ≤ 8

Subtract 16 from both-side of the inequality.

4x ≤ 8-16

4x≤ -8

Divide both-side of the inequality by 4

`\frac{\cancel{4}x}{\cancel{4}}\leq-(8)/(4)`

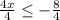
x ≤ -2

Combine the solutions.

-3 ≤ x ≤ -2

This can be written in interval notation as [-3, -2].