Question

Find the height of a rhombus whose diagonals are 40 mm and 30 mm.

Answer 1

We know that the area of a rhombus can be calculated as:

`A=(1)/(2)ab\text{ }`

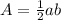
where a and b are the lengths of the diagonals.

Then the area of the rhombus is:

`A=(1)/(2)(40)(30)=600`

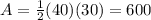
Now, we also know that the area can be obtained by:

`A=sh`

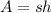
where s is the length of the side and h is the height. To obatain the height we need the length of the side. Then lenght of a rhombus is given by:

`s=\sqrt[]{((a)/(2))^2+((b)/(2))^2}`

Then ins this case we have:

`\begin{gathered} s=\sqrt[]{((40)/(2))^2+((30)/(2))^2} \\ s=\sqrt[]{625} \\ s=25 \end{gathered}`

Now that we know the lenght of the side we use the second formula for the area to get h:

`\begin{gathered} 25h=600 \\ h=24 \end{gathered}`

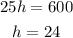
Therefore the height of the rhombus is 24 mm.