Question

an x-ray test is used to detect a certain disease that is common in 3% of the population the test has the following error 87 per-cent of people who are disease-free to get a positive reaction and 2% of the people who have the disease do get a negative reaction from the test a large number of people are screened at random using the test and those with a positive reaction are further examine what is the probability that a person tested at random indeed has the disease given that the test results shows positive

Answer 1

Let the event D be that a person has the disease.

`P(D)=(3)/(100),P(D^(\prime))=(97)/(100)`

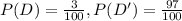
Now Let T be positive test and T' be a negative test result.

`P(T|D^(\prime))=(87)/(100),P(T|D)=(13)/(100),P(T^(\prime)|D)=(2)/(100),P(T^(\prime)|D^(\prime))=(98)/(100)`

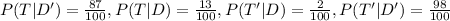
So the probability that the person has the disease given that the test is positive is given by:

`\begin{gathered} P(D|T)=(P(D)P(T|D))/(P(D)P(T|D)+P(D^(\prime))P(T|D^(\prime))) \\ =((3)/(100)*(13)/(100))/((3)/(100)*(13)/(100)+(97)/(100)*(87)/(100)) \\ =(13)/(2826) \\ \approx0.0046 \end{gathered}`

So only 0.46% of the people who tested positive will have the disease.