Question

The weekly salaries (In dollars) for 8 employees of a small business are given below.(Note that these are already ordered from least to greatest.)554, 626, 649, 702, 718, 855, 896, 1184Suppose that the $1184 salary changes to $968. Answer the following.(a) What happens to the median?(b) What happens to the mean?it decreases by s]It increases by siIt stays the same.It decreases by saIt increases by siIt stays the same.Х?

Answer 1

a) The Median stays the same

b) The Mean decreases by $27

Step-by-step explanation:

We were given the following weekly salaries:

`554,626,649,702,718,855,896,1184`

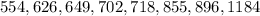
The mean & median for the data above is shown below:

`\begin{gathered} Mean=\frac{\text{Sum of elements}}{Number\text{ of elements}} \\ Mean=(554+626+649+702+718+855+896+1184)/(8) \\ Mean=(6184)/(8) \\ Mean=773 \\ \\ Median=(702+718)/(2) \\ Median=(1420)/(2) \\ Median=710\text{ (the middle number in the array)} \end{gathered}`

Suppose that the $1184 salary changes to $968, we have:

`\begin{gathered} Mean=\frac{\text{Sum of elements}}{Number\text{ of elements}} \\ Mean=(554+626+649+702+718+855+896+968)/(8) \\ Mean=(5968)/(8) \\ Mean=746 \\ \\ \text{The Median remains unchanged since the position of the salary changed is the same} \end{gathered}`

Therefore,

a) The Median stays the same

b) The Mean decreases by $27