Question

Two cars collide at an icy intersection and stick together afterward. The first car has a mass of 1750 kg and was approaching at 6.00 m/s due south. The second car has a mass of 700 kg and was approaching at 19.0 m/s due west.(a) Calculate the final velocity of the cars. (Note that since both cars have an initial velocity, you cannot use the equations for conservation of momentum along the x-axis and y-axis; instead, you must look for other simplifying aspects..)Magnitude m/sDirection ° (counterclockwise from west is positive)(b) How much kinetic energy is lost in the collision? (This energy goes into deformation of the cars.) J

Answer 1

Given:

• Mass of first car 1, m1 = 1750 kg

,

• Mass of second car, m2 = 700 kg

,

• Initial velocity of car 1, u1 = 6.00 m/s due south

,

• Initial velocity of car 2, u2 = 19.0 m/s due west.

Let's solve for the following:

• (a). Calculate the final velocity of the cars.

Apply the conservation of momentum.

In the West direction(x-direction), we have:

`\begin{gathered} m_1u_1+m_2u_2=(m_1+m_2)v_x \\ \\ 1750(0)+700(19.0)=(1750+700)v_x \\ \\ 13300=2450v_x \\ \\ v_x=(13300)/(2450) \\ \\ v_x=5.43\text{ m/s} \end{gathered}`

In the South direction (y-direction), we have:

`\begin{gathered} m_1u_1+m_2u_2=(m_1+m_2)v_y \\ \\ 1750(6.00)+700(0)=(1750+700)v_y \\ \\ 10500=2450v_y \\ \\ v_y=(10500)/(2450) \\ \\ v_y=4.29\text{ m/s} \end{gathered}`

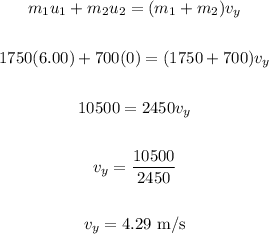
To find the magnitude, we have:

`\begin{gathered} v=√(v_x^2+v_y^2) \\ \\ v=√(5.43^2+4.29^2) \\ \\ v=√(29.4849+18.4041) \\ \\ v=√(47.889) \\ \\ v=6.92\text{ m/s} \end{gathered}`

To find the direction, apply the formula:

`\begin{gathered} \theta=tan^(-1)((v_y)/(v_x)) \\ \\ \theta=tan^(-1)((4.29)/(5.43)) \\ \\ \theta=tan^(-1)(0.79) \\ \\ \theta=38.31^o\text{ south of west} \end{gathered}`

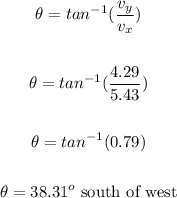
• (b). How much kinetic energy is lost in the collision?

To find the loss of kinetic energy, apply the formula:

`KE_(loss)=KE_(initial)-KE_(final)`

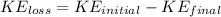
Using the Kinetic energy formula, we have:

`\begin{gathered} KE_(loss)=((1)/(2)m_1u_1^2+(1)/(2)m_2u_2^2)-(1)/(2)(m_1+m_2)v^2 \\ \\ KE_(loss)=((1)/(2)*1750*6.00^2+(1)/(2)*700*19^2)-((1)/(2)(1750+700)6.92^2) \end{gathered}`

Solving further:

`\begin{gathered} KE_(loss)=(31500+126350)-58660.84 \\ \\ KE_(loss)=157850-58660.84 \\ \\ KE_(loss)=99189.16\text{ J} \end{gathered}`

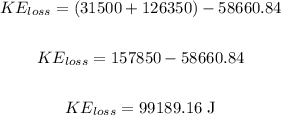
Therefore, the amount of kinetic energy lost is 99189.16 J.

• ANSWER:

(a). Magnitude = 6.92 m/s

Direction = 38.31° South of West

(b). 99189.16 J.