Question

An airplane travels 4472 kilometers against the wind in 8 hours and 5112 kilometers with the wind in the same amount of time. What is the rate of the plane instill air and what is the rate of the wind?Rate of the plane in still air:Rate of the wind:

Answer 1

From the information given, let the speed of the plane in still air be s, and let the speed of the wind be w.

This mean the speed against the wind would be represented by (s - w). Therefore, we would have;

`8(s-w)=4472`

Also, the airplane travels with the wind for the same amount of time, that is 8 hours. This too would be represented by (s + w). We would now have;

`8(s+w)=5112`

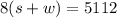
We now have a pair of simultaneous equations which would be solved as follows;

`\begin{gathered} 8(s-w)=4472---(1) \\ 8(s+w)=5112---(2) \\ \text{Divide both sides of equations (1) and (2) by 8 and we'll have;} \\ s-w=559---(3) \\ s+w=639---(4) \\ S\text{ubtract equation (3) from (4); } \\ 2w=80 \\ \text{Divide both sides by 2;} \\ w=40 \end{gathered}`

Having calculated w = 40, we now know that the speed of the wind is 40Kmph. We shall now calculate the rate of the plane in still air as follows;

`\begin{gathered} \text{From equation (3);} \\ s-w=559 \\ \text{Where w}=40 \\ s-40=559 \\ \text{Add 40 to both sides;} \\ s=599 \end{gathered}`

This means the rate of the plane in still air is 599 Kmph.

ANSWER:

Rate of the plane in still air: 599 Kmph

Rate of the