Question

Serial numbers for a product are to be made using 3 letters followed by 3 digits. The letters are to be taken from the first 8 letters of the alphabet, with norepeats. The digits are taken from the 10 digits (0, 1, 2, ..., 9), with no repeats. How many serial numbers can be generated?

Answer 1

The serial number of the product would look like XXX-### where XXX represents the letters and ### represents the number. The letter part of the serial number will be taken from the first 8 letters of the alphabet. To know how many different arrangements of letters can be done, we will be using permutation. The permutation equation is described as

`P(n,r)=\frac{n!}{(n-r)!_{}}_{}`

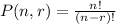
For the permutation of 3 letters, r = 3, for n = 8, the number of possible arrangements is

`P=(8!)/((8-3)!)=336`

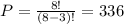
In a similar manner, we can pick 3 digits out of the 10 digits and arrange them in several manners using the permutation equation. For the digit part, we have r = 3 and n = 10. Computing for the number of possible arrangements for the digit part of the serial number, we have

`P=(10!)/((10-3)!)=720`

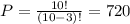
Finally, to get the overall number of serial numbers that can be generated, let's just multiply the permutation for both letters and digits. We get

`336*720=241920`

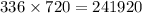
Therefore, there are 241920 serial numbers that can be generated.