First, find the inverse function of f(x). To do so, replace y=f(x) and isolate x from the equation:
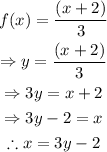
Swap x and y to find the inverse function:
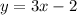
Replace y=f¨-1(x):
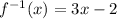
Notice that the inverse function is written in slope-intercept form, and the coefficient of the variable x is the slope. In this case, the coefficient of x is 3.
Therefore, the slope of the inverse function of f(x) is 3.