Step-by-step explanation
From the statement, we know that there are two possible scenarios:
A) Kira rolls the die and gets a face with a 1, 2, 3, 4, 5 or 6.
• The probability of this event is P(A) = 1/12.
,
• Kira will write the number of the face in this case.
B) Kira rolls the die and gets an edge.
• The probability for this event is 1/24.
,
• Kira will write the sum of the numbers that share the top edge.
,
• There are multiple values for the result of the sum.
We must take into account that:
• 1 and 5 are on opposite faces,
,
• 2 and 3 are on opposite faces,
,
• 4 and 6 are on opposite faces.
The possible values of the sum and the forms to get it are:
0. 3, = 1 + 2 → P(B'_1) = 1/24
,
1. 4, = 1 + 3 → P(B'_2) = 1/24
,
2. 5, = 1 + 4 → P(B'_3) = 2/24
,
3. 6, = 2 + 4 → P(B'_4) = 2/24
,
4. 7, = 1 + 6 = 2 + 5 = 3 + 4 → P(B'_5) = 3/24
,
5. 8, = 2 + 6 = 3 + 5 → P(B'_6) = 2/24
,
6. 9, = 3 + 6 = 4 + 5 → P(B'_7) = 2/24
,
7. 11, = 5 + 6 → P(B'_9) = 1/24
We have 8 possible results for the sum.
---------------------
Now, we want to know the value of the expected value of the numbers recorded by Kira.
By definition, the expected value is calculated by multiplying each of the possible outcomes by the likelihood that each outcome will occur and then summing all of those values.
The expected value of the number recorded by Kira will be:
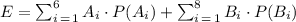
Where:
• A_i represents the result of event A_i and P(A_i) its probability,
,
• B_i represents the result of event B_i and P(B_i) its probability.
Using the data from above, we compute each of the sums.
A) For the first sum, we take into account that each event A_i has the same probability:
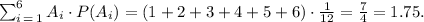
B) For the second sum, we use each of the values of the sum and the probabilities of each sum:
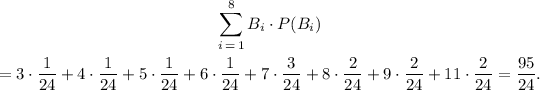
Summing the results of each sum, we get the following result for the expected value:
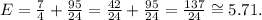
Answer
The expected value for the number recorded is 137/24 or approximately 5.71.