Question

Differentiate the following functions s=4e^3t-e^-2.5 w.r.t.t

Answer 1

`\displaystyle (ds)/(dt) = 12e^(3t)`

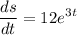
General Formulas and Concepts:

Algebra I

• Functions
• Function Notation

Calculus

Derivatives

Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Derivative Property [Addition/Subtraction]:
`\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]`

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

eˣ Derivative:
`\displaystyle (d)/(dx) [e^u]=e^u \cdot u'`

Explanation:

Step 1: Define

Identify

`\displaystyle s = 4e^(3t) - e^(-2.5)`

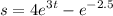
Step 2: Differentiate

1. eˣ Derivative:
   `\displaystyle (ds)/(dt) = 4e^(3t) \cdot (d)/(dt)[3t] - (d)/(dt)[e^(-2.5)]`
2. Basic Power Rule:
   `\displaystyle (ds)/(dt) = 4e^(3t) \cdot 3t^(1 - 1) - 0`
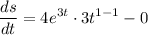
3. Simplify:
   `\displaystyle (ds)/(dt) = 12e^(3t)`

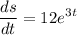
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Derivatives

Book: College Calculus 10e