a) The factors have the form:
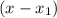
where x1 is a zero of the function. A zero is a point at which the graph intercepts the x-axis. From the graph, the zeros are:
-6, -4, 2, and 3
Therefore, the factors are:
(x + 6)
(x + 4)
(x - 2)
(x - 3)
b) Multiplying all these factors we get a polynomial, p(x), with the zeros of the graph. That is:
p(x) = (x + 6)(x + 4)(x - 2)(x - 3)
c) Yes, it is possible to find other polynomials with the same zeros. To do that we have to multiply p(x) by a constant. For example, multiplying by 2:
f(x) = 2(x + 6)(x + 4)(x - 2)(x - 3)
and f(x) has the same zeros as p(x)
d) Every polynomial obtained in the previous way, multiplying p(x) by a constant, will have a different graph. In conclusion, it is not possible to find other polynomials with the same zeros and the same graph.