Question

If A( x, 1), B( -3,7), C( -5, 9), and D( 5, 4), find the value of x so that lines are parallelPoints A and B belong to one line and points C and D belong to another line

Answer 1

we are given points A and B that belong to a line and points B and C that belong to another line that is parallel to the first one. We will first find the line that goes through points B and C. First, we will find the slope of this line, using the following formula:

`m_2=(y_2-y_1)/(x_2-x_1)`

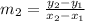
We have the following points:

`\begin{gathered} (x_1,y_1)=(-5,9) \\ (x_2,y_2)=(5,4) \end{gathered}`

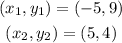
replacing in the equation, we get:

`m_2=(4-9)/(5-(-5))=-(5)/(10)=-(1)/(2)`

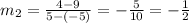
Since the lines are parallel, we have the following relationships between the slopes of each line:

`m_1=-(1)/(m_2)`

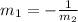
replacing the known values we get:

`m_1=-(1)/((-(1)/(2)))=2`

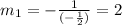
Now we can apply the formula for the slope of these lines, using the following points:

`\begin{gathered} (x_1,y_1)=(x,1) \\ (x_2,y_2)=(-3,7) \end{gathered}`

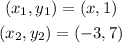
Replacing the known values we get:

`m_1=(7-1)/(-3-x)`

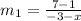
replacing the value for the slope:

`2=(7-1)/(-3-x)`

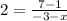
Now we will solve for "x", first by solving the operation in the numerator:

`2=(6)/(-3-x)`

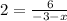
now we will multiply by the expression in the denominator on both sides:

`2(-3-x)=(6)/(-3-x)(-3-x)`

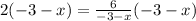
Simplifying:

`-6-2x=6`

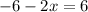
Now we will add 6 on both sides:

`\begin{gathered} -6+6-2x=6+6 \\ -2x=12 \end{gathered}`

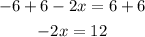
Now we will divide by "-2"

`x=(12)/(-2)=-6`

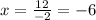
Therefore, the value of "x" for the two lines to be parallel is -6