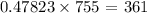Question

The amount of time a certain brand of light bulb lasts is normally distribued with a mean of 1300 hours and a standard deviation of 20 hours. Out of 755 freshly installed light bulbs in a new large building, how many would be expected to last than 1330 hours, to the nearest whole number?

Answer 1

361 light bulbs out of the 755 will last over 1330 hours

Here, we want to calculate the expected number of bulbs

The first thing we have to do here is to calculate the z-score

We have this as follows;

`\begin{gathered} z\text{ = }\frac{x-\mu}{\frac{\sigma}{\sqrt[]{n}}} \\ x\text{ = 1330 hours} \\ \mu\text{ = 1300 hours (mean)} \\ \\ \sigma\text{ = 20 hours ( standard deviation)} \\ n\text{ = 755} \\ \\ z\text{ = }\frac{1330-1300}{\frac{20}{\sqrt[]{755}}}\text{ = 0.0546} \end{gathered}`

Now, we have to calculate the probability that is equal to this z-score

So, the probability we want to calculate is that which is greater than the calculated z-score

`P\text{ (z > 0.0546)}`

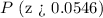
We are going to use the standard normal distribution table here

By using the table, we have the equivalent probability as 0.47823 (about 48%)

So, out of the 755 freshly installed light bulbs, 47.823% will last more than 1330 hours

The exact number that will last will be;

`0.47823*755\text{ = 361}`