The product of two consecutive odd integers is 899.
Let x be the first odd integer.
Then (x+2) will be the second odd integer.
Their product must be equal to 899, so we can write
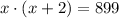
Simplify the equation
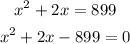
This is a quadratic equation that can be solved by either factoring or using the quadratic formula.
Let's use the quadratic formula.

For the given case, the coefficients are
a = 1
b = 2
c = -899
![\begin{gathered} x=\frac{-2\pm\sqrt[]{2^2-4(1)(-899)}}{2(1)} \\ x=\frac{-2\pm\sqrt[]{3600}}{2} \\ x=(-2\pm60)/(2) \\ x=(-2+60)/(2),\; x=(-2-60)/(2) \\ x=(58)/(2),\; x=(-62)/(2) \\ x=29,\; x=-31 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/11toryhid3di7jtk30lh.png)
So, the first integer is 29
The second odd integer is x + 2 = 29 + 2 = 31
Verify the results
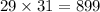
Also, -31 is the first integer.
The second integer is x + 2 = -31 + 2 = -29
Verify the results
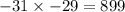
Therefore, the solution is
