Question

1. Find the distance between the line and the point Exercises 11.8 Complete the following: (b) 7x - (d) (f) 3. (a) 3x + 4y = 24: (-10, 1) (c) x + 2y = 12; (4, -6) (e) + 3y = 0; (1, -7) for or find the length of one altitude and the area of the (b) A-4letter a from question 1

Answer 1

The formula to find the distance between a point and a line is

`\begin{gathered} d=|\frac{Ax_p+By_p+C}{\sqrt[]{A^2+B^2}}| \\ \text{ For} \\ Ax+By+C=0 \\ \text{ Where} \\ x_p\text{ is the x coordinate of the point} \\ y_p\text{ is the y coordiante of the point} \end{gathered}`

Graphically

So, in this case, you have

`\begin{gathered} Ax+By+C=0\Leftrightarrow3x+4y-24=0 \\ P(-10,1) \end{gathered}`

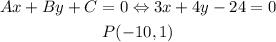
Then

`\begin{gathered} A=3 \\ B=4 \\ C=-24 \\ x_p=-10 \\ y_p=1 \\ d=|\frac{3\cdot(-10)+4\cdot1-24}{\sqrt[]{(3)^2+(4)^2}}| \\ d=|\frac{-30+4-24}{\sqrt[]{9^{}+16}}| \\ d=|\frac{-50}{\sqrt[]{25}}| \\ d=|(-50)/(5)| \\ d=|-10| \end{gathered}`

The absolute value is the distance between a number and zero. The distance between -10 and 0 is 10.

`d=10`

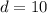
Therefore, the distance between the point of the line is 10 units.