Question

68829If PQRS is a quadrilateral inscribed in a circle, then the opposite angles of the quadrilateral areii) The values of r and y aredegrees anddegrees resp

Answer 1

An inscribed quadrilateral is any four-sided figure whose vertices all lie on a circle.

This conjecture gives a relation between the opposite angles of such a quadrilateral. It says that these opposite angles are in fact supplements for each other. In other words, the sum of their measures is 180 degrees.

Therefore, we can say that:

`\text{ x + }82^(\circ)=180^(\circ)`
`\text{ y + }68^(\circ)=180^(\circ)`

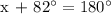
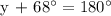
a.) Let's determine the value of x.

`\text{ x + }82^(\circ)=180^(\circ)`
`\text{ x }=180^(\circ)\text{ - }82^(\circ)`
`\text{ x }=98^(\circ)`

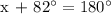
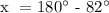
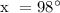
b.) Let's determine the value of y.

`\text{ y + }68^(\circ)=180^(\circ)`
`\text{ y }=180^(\circ)\text{- }68^(\circ)`
`\text{ y }=112^(\circ)`

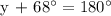
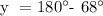
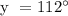
Therefore, x = 98° and y = 112°.

The opposite angles of the inscribed quadrilateral are Supplementary.