Take into account that the momentum must conserve before and after the collision.
Before the collision the total momentum is:
![\begin{gathered} p_o=p_1-p_2 \\ p_o=m_1v_1-m_2v_2 \\ p_o=(4kg)(4(m)/(s))-(6kg)(6(m)/(s)) \\ p_o=16\operatorname{kg}(m)/(s)-36\operatorname{kg}(m)/(s)=-20\operatorname{kg}(m)/(s) \end{gathered}]()
p1 and p2 have opposite signd because the carts are moving in opposite directions. If motions to the right is considered as positive, then, the previous negative result means that total momentum beofre the collision is to the left.
Now, after the collision you obtain:
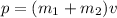
v is the speed of the cart together after the collision. Due to the momentum must conserve, po = p, then by solving for v and replacing, you have:
![\begin{gathered} p=p_o=(m_1+m_2)v \\ v=(p_o)/(m_1+m_2) \\ v=\frac{-20\operatorname{kg}(m)/(s)}{4\operatorname{kg}+6\operatorname{kg}} \\ v=-2(m)/(s) \end{gathered}]()
the speed of the carts togueter is 2m/s and the direction of motion is to the left.