Question

I am on the roof of a 1200ft building, and I am looking at an even taller skyscraper. I have an inclinometer. WhenI look up at the top of the skyscraper, my inclinometer reads that I am looking up at an angle of elevation of35 degrees above the horizontal. When I look down at the base of the skyscraper, my inclinometer reads that Iam looking down at an angle of depression of 60 degrees below the horizontal. I also know that the building andskyscraper are 600 ft apart. Find the height of the skyscraper in exact and approximate form.

Answer 1

Let's try to draw a rough diagram of the problem:

From here, we can dissect a triangle as shown below:

From this diagram, we are going to find H, the height of the skyscraper.

We already know that part of the side length "H" is 1200 feet. We need to find the other part of "H". Let's label it h1.

Finding h1:

`\begin{gathered} \tan 35=(h1)/(600) \\ h1=600\tan 35 \\ h1=420.12 \end{gathered}`

Thus,

`\begin{gathered} H=h1+1200 \\ H=420.12+1200 \\ H=1620.12 \end{gathered}`

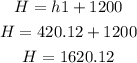
The height of the skyscraper is 1620.12 feet