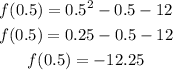Question

Graph the function f(x) = x²-x-12 on the coordinate plane.

Answer 1

x-intercepts= (-3,0) and (4,0)

y-intercept= (0,-12)

minimum= (0.5 , -12.25)

Step-by-step explanation

Factoring we get:

`x^2-x-12=(x+3)(x-4)`

For y-intercepts (y=0):

`\begin{gathered} x+3=0 \\ x=-3 \end{gathered}`

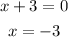
and

`\begin{gathered} x-4=0 \\ x=4 \end{gathered}`

for x-intercepts (x=0):

`\begin{gathered} f(0)=0^2-0-12 \\ f(^0)=-12 \end{gathered}`

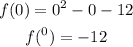
the minimum must be at the value of x in the middle of -3 and 4, this is 0.5, and replacing:

`\begin{gathered} f(0.5)=0.5^2-0.5-12 \\ f(0.5)=0.25-0.5-12 \\ f(0.5)=-12.25 \end{gathered}`