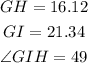Question

I need help solving this problem. It is solving right triangles

Answer 1

To solve the triangle, we shall begin by applying the ratios of right triangle given one indicated angle and one (or two) sides.

Note that the angle given is 41 degrees. This means the opposite side is 14. The opposite side is that which faces the reference angle. The hypotenuse is the longest side, that is, the side which is facing the right angle. The adjacent is the side that lies between the reference angle and the right angle.

Therefore;

`\begin{gathered} \text{Opposite}=14 \\ \text{Adjacent}=GH \\ \text{Hypotenuse}=GI \end{gathered}`

We shall start by calculating the hypotenuse as follows;

`\begin{gathered} \text{Given the opposite (14 units) and the hypotenuse (GI), we would have;} \\ \sin \theta=(opp)/(hyp) \\ \sin 41=(14)/(GI) \\ \text{Cross multiply and you'll have;} \\ GI=(14)/(\sin 41) \\ GI=(14)/(0.6560590) \\ GI=21.3395\ldots \\ GI\approx21.34 \end{gathered}`

Next, we solve for the side GH (adjacent), as follows;

`\begin{gathered} \tan \theta=(opp)/(adj) \\ \tan 41=(14)/(GH) \\ \text{Cross multiply and you'll have;} \\ GH=(14)/(\tan 41) \\ GH=(14)/(0.8692867) \\ GH=16.105158\ldots \\ GH\approx16.12 \end{gathered}`

Observe also that one angle is 90 degrees while another is 41 degrees. Therefore the third angle is;

`\begin{gathered} \angle G+\angle H+\angle I=180\text{ \lbrack{}Sum of angles in a triangle\rbrack} \\ 41+90+\angle I=180 \\ 131+\angle I=180 \\ \text{Subtract 131 from both sides;} \\ \angle I=49 \end{gathered}`

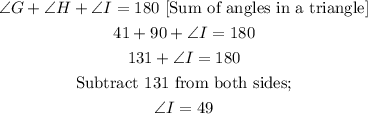
ANSWER:

`\begin{gathered} GH=16.12 \\ GI=21.34 \\ \angle GIH=49 \end{gathered}`