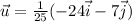Question

Topic is hard for me to understand, help is appreciated

Answer 1

Given vector v is,

`\vec{v}=-24\vec{i}-7\vec{j}`

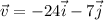
$$=-24\vec{i}-7\vec{j}$$To find the unit vector that has the same direction as the vector v is,

Unit vector u is,

`\vec{u}=\frac{\vec{v}}{\lvert\vec{v}\rvert}-----(1)`

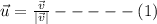
we have that,

To find a unit vector with the same direction as a given vector, we divide the vector by its magnitude.

The magnitude of a vector formula is used to calculate the length of a vector and is denoted by |v|. The magnitude of a vector is always a positive number or zero it cannot be a negative number.

`\lvert x\vec{i}+y\vec{j}\rvert=\sqrt[]{x^2+y^2}`

we get,

`\lvert\vec{v}\rvert=\sqrt[]{24^2+7^2}`
`=\sqrt[]{625}`
`=25`
`\lvert\vec{v}\rvert=25`

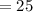
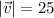
Substitute the values in equation (1), we get

`\vec{u}=\frac{-24\vec{i}-7\vec{j}}{25}`
`\vec{u}=(1)/(25)(-24\vec{i}-7\vec{j})`

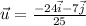
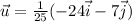
Answer is:

`\vec{u}=(1)/(25)(-24\vec{i}-7\vec{j})`