Question

A model rocket accelerated upwards at 3.80 m / s² from the ground. The small motor runs for 9.40s before breaking down.The rocket continues in a free fall motion until it collides with the ground.1)What is the speed of the rocket when it breaks down.2)What is its maximum altitude3)What is the total flight time

Answer 1

1) In order to determine the speed of the rocket when it breaks down, use the following formula:

`v=v_o+at`

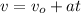
where,

vo: initial speed = 0m/s

a: acceleration = 3.80 m/s^2

t: time = 9.40s

Replace the previous values of the parameters into the formula for v:

`v=(0m)/(s)+((3.80m)/(s^2))(9.40s)=(35.72m)/(s)`

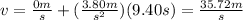
Hence, when the rocket breaks down it speed is 35.72 m/s

2)

Use the following formula to determine the vertical distance traveled by the rocket after it breaks down:

`y=(v^2_0-v^2)/(2g)=(((35.72m)/(s))^2-((0m)/(s))^2)/(2((9.8m)/(s^2)))=65.1m`

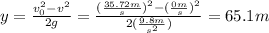
where the intial speed vo , in this case, is the final speed of the first trajectory.

Now, consider the distance traveled by the rocket before it breaks down. Us the following formula:

`v^2=v^2_o+2ay_o`

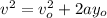
where v is the final speed of the rocket in the first trajectory (35.72m/s), vo is the initial speed of the rocket in the first trajectory (vo = 0m/s becasue it started its motion from rest on the ground) and a is 3.80m/s^2.

Solve the previous equation for yo and replace the rest of the parameters:

`y_o=(v^2-v^2_0)/(2a)=(((35.72m)/(s))^2-((0m)/(s))^2)/(2((3.80m)/(s^2)))=167.88m`

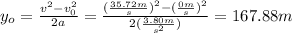
The maximum height of the rocket is:

hmax = yo + y = 167.88m + 65.1m = 232.98 m

3) Take into account that when the rocket breaks down it keeps going up until its speed is 0 m/s. in this case, use the following formula:

`v=v_o-gt`

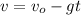
to get the time at which the speed of the rocket is zero. In this case, you have:

vo = 35.72 m/s (the initial speed is the final speed of the first trajectory)

g: gravitational acceleration constant = 9.8m/s^2

v = 0 m/s

`t=(v_o-v)/(g)=((35.72m)/(s)-(0m)/(s))/((9.8m)/(s^2))=3.64s`

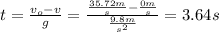
Furthermore, consider that the rocke falls down in free fall when it reachs the maximum height. To determine the time it takes to reach the ground, use the following formula:

`h_(\max )=(1)/(2)gt^2`

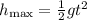
Solve the previous equation for t and resplace the values of g and hmax:

`t=\sqrt{(2h_(\max))/(g)}=\sqrt[]{(2(232.98m))/((9.8m)/(s^2))}=6.89s`

Finally, consider that you have to consider the time before the rocket breaks down, the time before the rocket speed becomes zero and the time the rocket takes to reach the ground in freee fall.

Then, the total flight time is:

total time = 9.40s + 3.64s + 6.89s = 19.93s