Step-by-step explanation
Albert) Let's define
![\begin{cases}A=\text{ money earned from 1000 dollars and 1.2\% of annual interest compounded monthly,} \\ L=\text{ 2\% of 500 dollars, lost over the course of the ten years,} \\ B=\text{ money earned from 500 dollars growing compounded continuously at a rate of 0.8\% annually.}\end{cases}]()
Then,
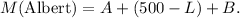
To calculate A, we have the following compound interest formula:
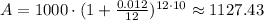
L is easy to calculate:
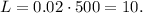
To calculate B, we have a formula as well:
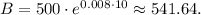
Then,

Answer
The balance of Albert's $2000 after ten years is $2159.07.