Question

Cody has some quarters and dimes. He has 24 coins worth a total of $3.60 . How many of each type of coin does he have?

Answer 1

Step-by-step explanation:

Here, we want to find the number of each type of coin

Let the number of quarters be q and the number of dimes be d

The sum of these two is 24

Mathematically, that would be:

`q+d\text{ = 24}`

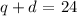
While a quarter is worth 25 cents, a dime is worth 10 cents

Since $1 = 100 cents

The total number of cents in $3.60 is 3.60 * 100 = 360 cents

For q quarters, we have a total value of 25 * q = 25q cents

For d dimes, we have a total of 10 * d = 10d cents

The sum of both is 360 cents

We have that mathematically as:

`25q\text{ + 10d = 360}`

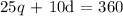
We thus have the following system of linear equations to solve:

`\begin{gathered} q\text{ + d = 24} \\ 25q\text{ + 10d = 360} \end{gathered}`

From the first equation in the system:

`d\text{ = 24-q}`

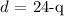
Substitute this into the second equation, we have it that:

`\begin{gathered} 25q\text{ + 10(24-q) = 360} \\ 25q\text{ + 240-10q = 360} \\ 25q-10q\text{ = 360 - 240} \\ 15q\text{ = 120} \\ q\text{ = }(120)/(15) \\ q\text{ = 8} \end{gathered}`

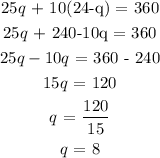
Now, to get d, we simply subtract this value from 24

Mathematically, that would be:

`\begin{gathered} d\text{ = 24-8} \\ d\text{ = 16} \end{gathered}`

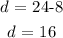
He has 8 quarters and 16 dimes